1. Bubble Sort (버블 정렬)
- 두 인접한 원소를 검사하여 정렬하는 방법이다.
- 시간 복잡도는 O(n^{2})로 매우 느리다. (효율성은 나쁘지만 코드가 단순하기 때문에 교육용으로(?) 자주 사용되는 것 같다.)
- Stable 하고 In-place 하다. (https://blog.wookingwoo.com/27 참고)
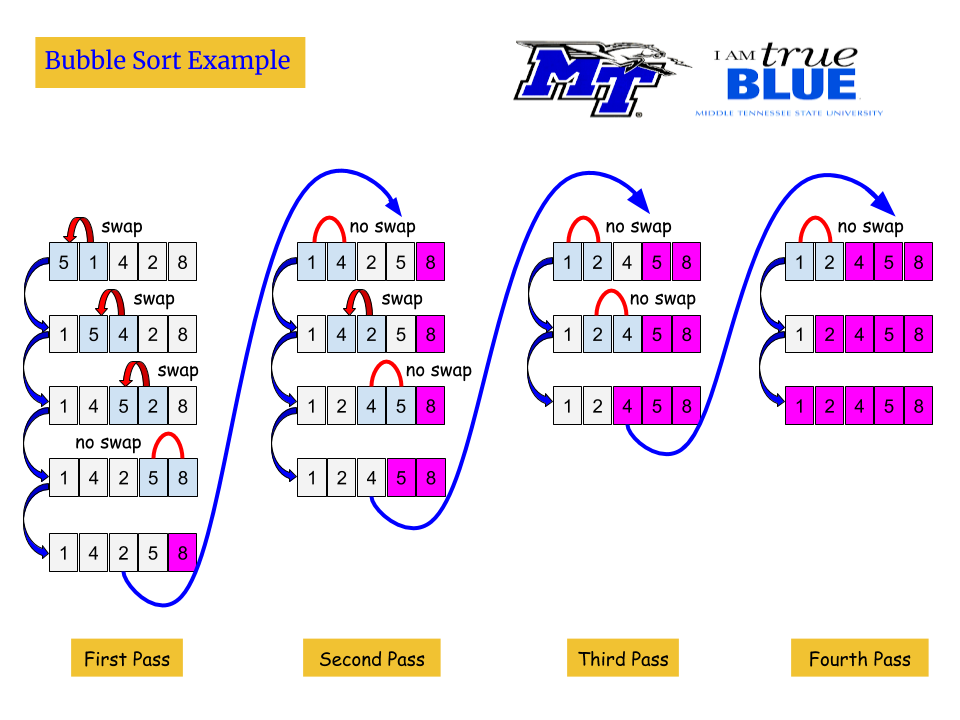
이미지 출처: https://www.cs.mtsu.edu/~xyang/2170/bubbleSort.html
| Bubble Sort Complexity | |
| Average (평균 시간복잡도) | O(n^2) |
| Best Case (최선 시간복잡도) | O(n) |
| Worst Case (최악 시간복잡도) | O(n^2) |
| Space Complexity (공간복잡도) | O(1) |
C++ 코드 예시
void swap(int *xp, int *yp) {
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n-1; i++)
for (j = 0; j < n-i-1; j++)
if (arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}
2. Cocktail Shaker Sort (칵테일 셰이커 정렬),
Bidirectional Bubble Sort (양방향 거품 정렬)
- Bubble sort의 단점(거북이 데이터 발생)을 개선
- Bubble sort의 각 pass를 한 번은 왼쪽에서 오른쪽으로, 그다음에는 오른쪽에서 왼쪽으로 실행한다.
- 입력 데이터가 많이 정렬되어 있는 상태라면 빠르게 정렬할 수 있다.
- Stable 하고 In-place 하다.
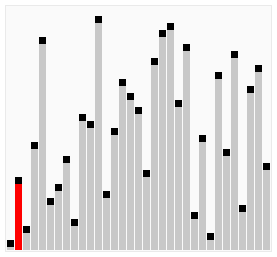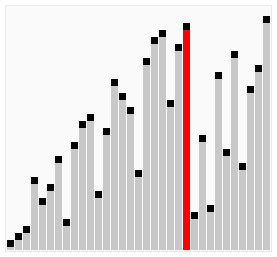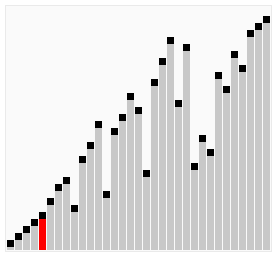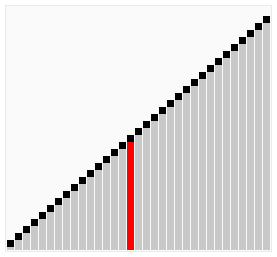
이미지 출처: https://ko.wikipedia.org/wiki/칵테일_정렬
| Cocktail Shaker Sort Complexity | |
| Average (평균 시간복잡도) | O(n^2) |
| Best Case (최선 시간복잡도) | O(n) |
| Worst Case (최악 시간복잡도) | O(n^2) |
| Space Complexity (공간복잡도) | O(1) |
3. Comb Sort (빗질 정렬)
- bubble sort에서 거북이(tutle) 데이터를 줄이고자 고안되었다.
- bubble sort에서는 인접한 두 데이터의 크기를 비교한다. (비교하는 두 데이터의 거리를 gap이라고 한다. bubble sort에서는 gap이 1인 셈이다.)
- gap의 크기는 1보다 크게 하며 bubble sort의 각 pass가 진행됨에 따라 gap의 크기를 줄여나간다.
- gap의 크기에 따라comb sort의 효율성이 달라지며 1.3이 권장된다.
- Not Stable 하며 In-place 하다.

이미지 출처: https://parodev.tistory.com/44
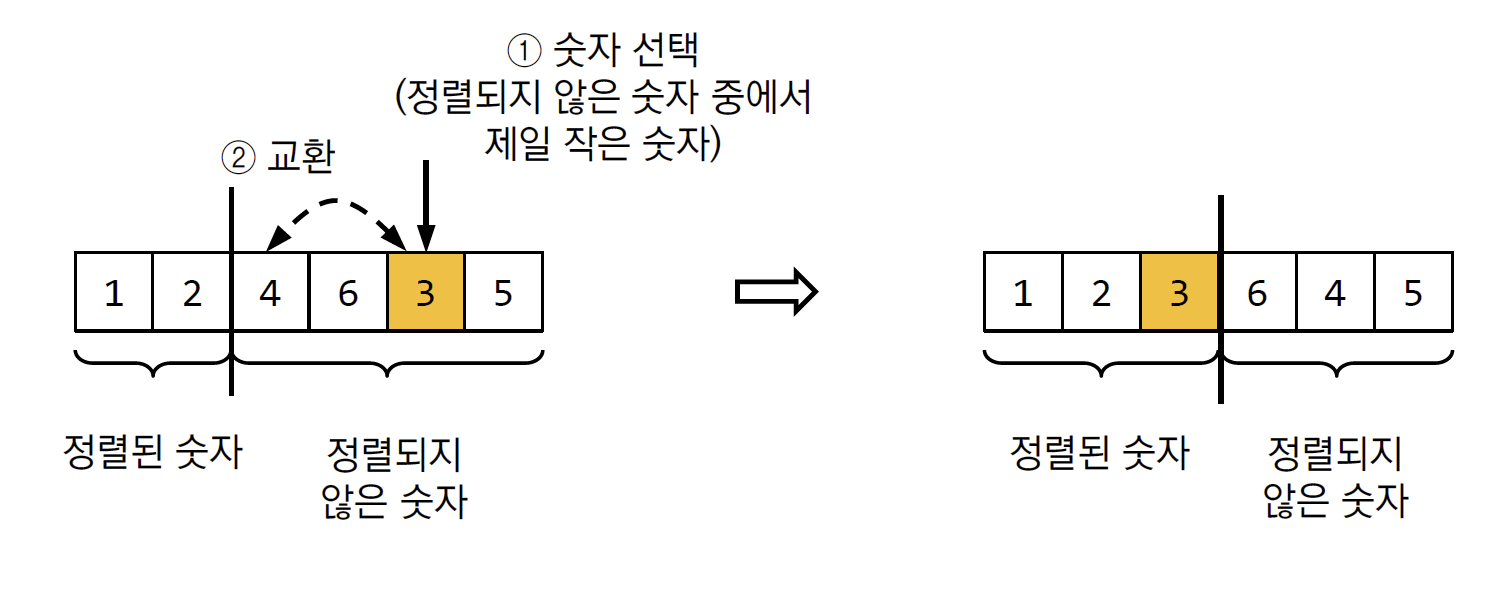
4. Selection Sort (선택 정렬)
- 정렬 중간 과정에 데이터가 두 부분으로 나누어진다.
- 왼쪽에는 정렬 된 데이터를 보관하며 오른쪽에는 정렬이 되지 않은 데이터를 보관한다.
- 오른쪽 데이터에서 제일 작은 데이터를 검색하여 선택하고 오른쪽 데이터의 제일 앞 숫자를 그 숫자를 교환한다.
- Not Stable 하며 In-place 하다.

5. Insertion Sort (삽입 정렬)
- 정렬 중간 과정에 데이터가 두 부분으로 나누어진다.
- 왼쪽에는 정렬이된 데이터가 있으며 오른쪽에는 정렬이 되지 않은 데이터가 온다.
- 오른쪽 데이터의 제일 앞 숫자를 그 왼쪽의 정렬된 데이터의 제 위치에 삽입한다. 이 과정에서 중간의 모든 데이터는 오른쪽으로 한 칸씩 이동시킨다.
- Stable 하고 In-place 하다.

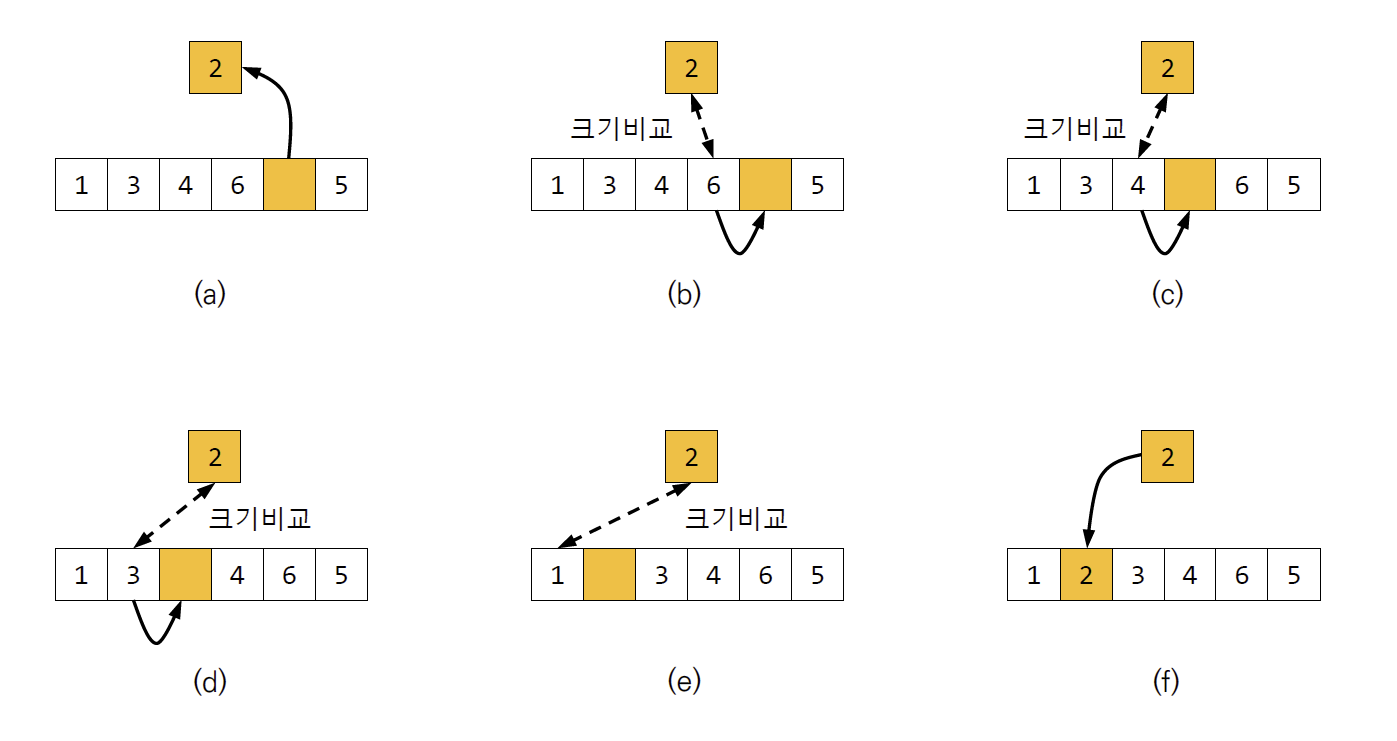
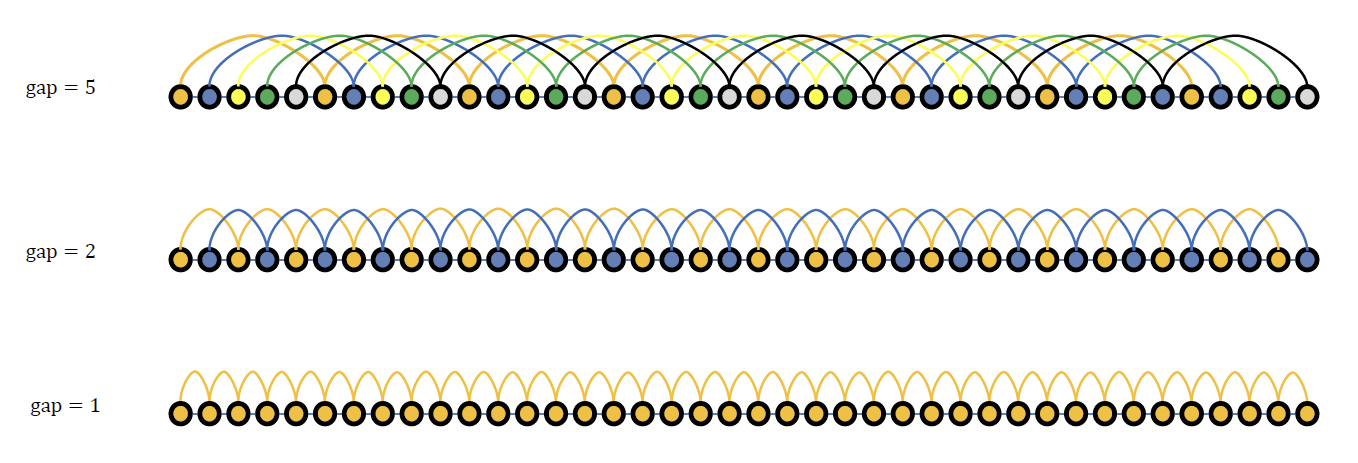
6. Shell Sort (셸 정렬)
- 1959년 Donald Shell가 개발했다.
- Insertion sort를 기본 아이디어로 한다.
- 서로 멀리 떨어져있는 숫자들을 insertion sort로 정렬하기 시작하고, 점점 두 숫자들 사이의 거리(gap)를 좁혀서 정렬한다.
- 최종적으로 gap=1 이 되면, 원래의 insertion sort를 실행하는 것과 동일해진다.
- 미리 gap>1 단계에서 거북이 데이터를 목표 위치 근처로 많이 이동시켜 놓았으므로 이 단계 시작 전에는 정렬된 상태에 많이 가까운 상태이다.
- gap의 크기에 따라 Shell sort의 효율성이 달라진다.
- Not Stable 하며 In-place 하다.
7. Merge Sort (합병 정렬)
- 분할정복 사용
- 모든 숫자들을 독립적으로 분할
- 그룹별로 원소의 크기를 비교한 하나의 그룹으로 병합
- Not Stable 하며 In-place 하다.
| Merge Sort Complexity | |
| Average (평균 시간복잡도) | O(n × log n) |
| Best Case (최선 시간복잡도) | O(n × log n) |
| Worst Case (최악 시간복잡도) | O(n × log n) |
| Space Complexity (공간복잡도) | O(n) |
8. Quick Sort (퀵 정렬)
| Bubble Sort (버블 정렬) | Cocktail Shaker Sort (칵테일 셰이커 정렬) | Comb Sort (빗질 정렬) | Selection Sort (선택 정렬) | Insertion Sort (삽입 정렬) | Shell Sort (셸 정렬) | Merge Sort (합병 정렬) | Quick Sort (퀵 정렬) | |
| Average (평균 시간복잡도) | O(n^2) | O(n^2) | O(n log n) | |||||
| Worst Case (최악 시간복잡도) | O(n^2) | O(n^2) | O(n log n) | |||||
| Best Case (최선 시간복잡도) | O(n) | O(n) | O(n log n) | |||||
| Stable Sorting Algorithm (안정 정렬 알고리) | Stable | Stable | Stable | |||||
| In-place Algorithm | In-place | In-place | Not in-place | |||||
| 공간복잡도 | O(1) | O(1) | O(N) |
'프로그래밍 > 알고리즘 스터디' 카테고리의 다른 글
| [알고리즘] 회의실 배정 문제의 여러가지 풀이법 (Brute-Force, 분할정복, DP, 그리디) (0) | 2022.12.04 |
|---|---|
| [알고리즘] 최소 신장 트리(MST, Minimum Spanning Tree)와 Kruskal, Prim 알고리즘 (0) | 2022.12.03 |
| [알고리즘] Stable sorting algorithm, In-Place algorithm (0) | 2022.10.24 |


