회의실 배정 문제
회의실 배정 문제를 여러 가지 알고리즘으로 해석해보고자 한다.
문제의 상황은 아래와 같다.
실생활에서 자주 마주할만한 상황이라 재미있다.
회의실은 1개인데, n개의 회의가 있다.
이때 하나의 회의실에서 최대한 많이 회의를 할 수 있도록 스케줄을 잘 짜 보는 것이다.
(문제에서 S는 회의 시작시간, F는 회의 종료시간으로 주어진다.)
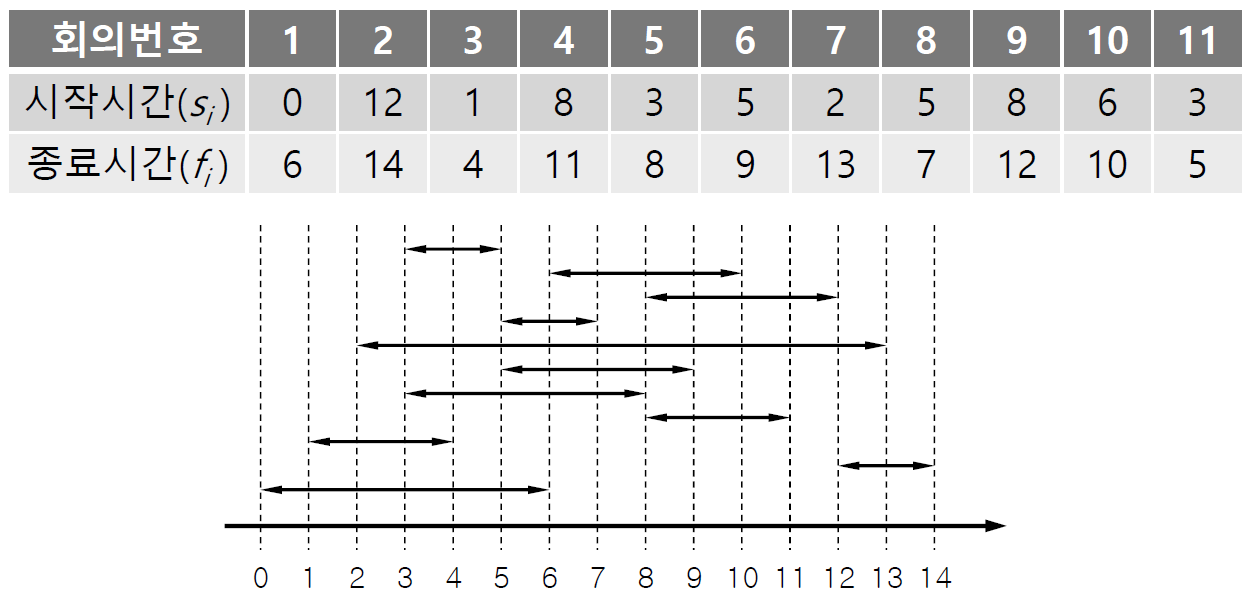
예를 들면 아래와 같은 상황이 있을 수 있다.
시간표를 어떻게 짜야 가장 많은 회의를 배정할 수 있겠는가? 한번 생각해보자.
백준 1931번에 비슷한 문제가 있으니 참고해도 좋다.
https://www.acmicpc.net/problem/1931
1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
여러 가지 방법으로 해결해볼 수 있을듯하다.
결론부터 말하면 가장 좋은 방법은 그리디 알고리즘을 사용하는 것이다.
단순 무식하지만 가장 직관적인 방법인 Brute-Force부터 알아보자.
Brute-Force
모든 경우의 수를 다 구해서 비교해보면 쉽다. (생각하기에만 쉽다. n이 조금만 커져도 경우의 수가 너무 많아지기 때문.)
모든 경우의 수를 구하려면 집합 S의 모든 부분집합을 계산해보면 된다.
모든 부분집합의 개수는 2^n개다. (각각의 회의가 포함될지, 안될지 2가지 경우씩 존재하기 때문)
이런.. n이 지수로 올라가버렸다. exponetial 하게 지수 시간 복잡도를 가지게 된다.
시간 복잡도: O(2^n)
재귀적 관계 분석
Brute-Force가 좋은 방법이 아니라는 것은 어느 정도 예상하고 있었다.
그렇다면 재귀적으로 분석해보자.
회의 Si와 Sj사이에 있는 회의를 Sij라고 설정해보자.
(이해하기 쉽게 간단히 기술했는데 조금 더 정확하게 설명하면 회의 Sij는 회의 Si가 종료한 이후에 시작하고, 회의 Sj가 시작하기 전에 종료되는 회의이다.)
그렇다면 회의 Sij에서 최적 값을 구해야 할 것이다.
여기서 최적 값이란 당연히 회의 Si에서 회의 Sj까지 개최할 수 있는 최대 회의 크기의 값을 말한다.
이 최적 값을 C(i, j)라고 설정해두자.
좀 복잡하게 나간 것 같은데 아래의 재귀적 관계를 만들기 위함이었다.
C(i, j) = C(i, k) + C(k, j) + 1
위의 식에서 k는 i와 j 사이에 있는 회의를 뜻한다.
k를 기준으로 둘로 나눴고 k는 빠져 잇기 때문에 1을 더해주었다.
오.. 뭔가 엄청난 식이 만들어졌다. 이제 드디어 재귀식을 만들 수 있게 된 것이다.
1) Sij = Ø 이면 C(i, j) = 0
2) Sij ≠ Ø 이면 C(i, j) = max { C(i, k) + C(k, j) + 1 }
Divide and Conquer (분할 정복)
이제 재귀식도 있겠다! 재귀 함수로 프로그래밍을 하면 된다.
하지만 단순히 분할 정복 기법을 사용한다면, overlapping subproblem이 발생하게 된다.
중복되는 부분이 많이 발생하는 것이다.
결국은 지수 시간이 걸리게 되는데 성능이 크게 좋아지지 않는다.
시간 복잡도: O(2^n)
Dynamic Programming (동적 계획법)
그렇다면 역시 DP이다. optimal substructure (최적 부분 구조)가 성립하기 때문이다.
앞의 재귀식을 보면 i, j, k로 3중 for문을 돌아야 한다.
시간 복잡도는 아래와 같이 나오게 될 것을 쉽게 유추할 수 있다.
시간 복잡도: O(n^3)
많이 좋아졌지만 3중 for문은 좀.. 그렇다.
더 효율적인 방법은 없을까? 그리디 알고리즘으로 접근해보자.
Greedy Algorithm (그리디 알고리즘, 탐욕 알고리즘)
문제의 상황으로 돌아가 다시 생각해보자.
과연 어떻게 설계를 해야 가장 좋은 스케줄을 짤 수 있을까?
몇 가지 선택지를 생각해볼 수 있다.
1) 가장 빨리 시작하는 회의부터 선택한다.
2) 가장 빨리 끝나는 회의부터 선택한다.
3) 가장 짧은 회의부터 선택한다.
4) 가장 적게 겹치는 회의부터 선택한다.
과연 어느 방법이 맞을까?
정답은.. 아래에 숨겨두었다.
정답은 2번이다.
가장 빨리 끝나는 회의부터 배정하는 것이 좋다.
우선 증명은 복잡하니 생략하고, 구현을 먼저 해보자.
greedy optimal substructure (탐욕적 부분 최적 구조)을 생각해보자.
모든 부분 문제에 대한 최적해를 찾지 않고, 최적해에 넣을 수 있는 한 개의 회의를 선택해보는 것이다.
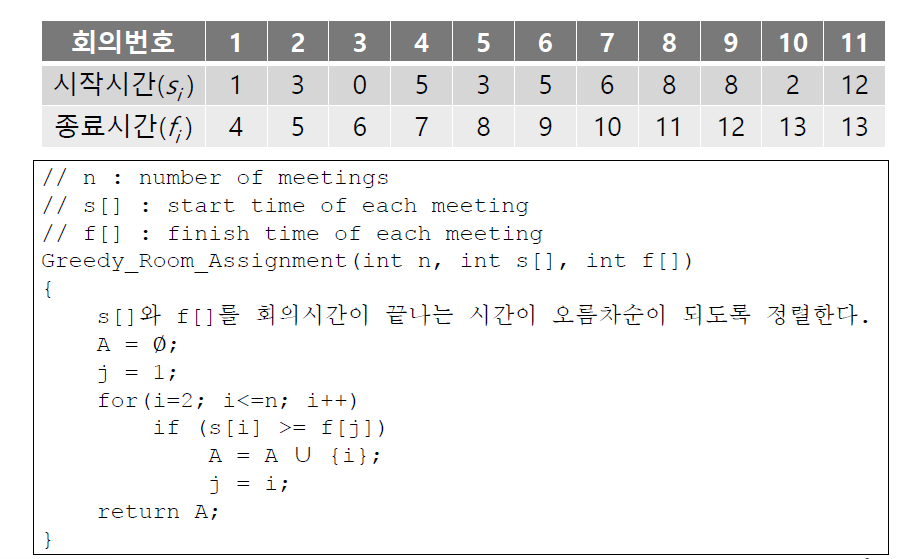
먼저 전처리 과정으로 회의 종료시간의 오름차순으로 회의를 정렬한다.
그렇게 되면 두 회의 ai, aj에 대해서 Fi <= Fj 일 때 Fi <= Sj라면 두 회의가 겹치지 않게 된다.
그리고 초기값 설정을 아래와 같이 해둔다.
1) A = Ø
2) j = 0
이제 그리디를 통해 S에서 가장 먼저 끝나는 회의를 선택해 집합 A에 추가할 수 있으면 추가하면 된다.
S의 모든 원소를 탐색했으면 종료한다.
파이썬으로는 아래와 같이 구현할 수 있다.


그렇다. 이렇게 그리디 접근법을 통해 해결하니 시간 복잡도가 O(n)이 나오게 되었다.
시간 복잡도: O(n)
그렇다면 그리디가 무조건 만능인가?
아쉽게도 그건 또 아니다.
문제 상황을 조금 바꾸어보겠다.
회의를 개최할 때 회의실 사용 비용을 받는다고 하고, 각각의 회의마다 서로 다른 비용을 주어준다.
이때 최대 비용이 발생하는 스케줄을 찾고자 한다면?
동전 계산문제와 동일한 상황이 된다.
그렇다면 그리디 접근법으로 해결할 수 없는 경우가 생기고 DP나 BackTracking을 사용해 해결해야 한다.
그리디 알고리즘은 정말 효율적인 알고리즘이지만 앞서 보았듯이 최적해에 대한 증명이 있어야 사용할 수 있다.
하지만.. 그 증명이 어렵다.. 그게 문제이다..
이번 상황에서는 왜 그리디 알고리즘을 사용할 수 있었을까?
궁금하면 아래의 증명을 잘 이해해보자!!

'프로그래밍 > 알고리즘 스터디' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리(MST, Minimum Spanning Tree)와 Kruskal, Prim 알고리즘 (0) | 2022.12.03 |
|---|---|
| [알고리즘] Stable sorting algorithm, In-Place algorithm (0) | 2022.10.24 |
| 정렬 알고리즘 총정리 (0) | 2022.10.24 |


